Advent Of Code 2020 Day 7: It's Bags All The Way Down
The puzzle for Day 7 resembles the closet where my family keeps various duffel bags: they’re all stuffed inside one another. The puzzle input is a set of production rules, like this:
light red bags contain 1 bright white bag, 2 muted yellow bags.
dark orange bags contain 3 bright white bags, 4 muted yellow bags.
bright white bags contain 1 shiny gold bag.
muted yellow bags contain 2 shiny gold bags, 9 faded blue bags.
shiny gold bags contain 1 dark olive bag, 2 vibrant plum bags.
dark olive bags contain 3 faded blue bags, 4 dotted black bags.
vibrant plum bags contain 5 faded blue bags, 6 dotted black bags.
faded blue bags contain no other bags.
dotted black bags contain no other bags.
Part 1 asks for how many different outermost bags could end up
carrying a gold bag. One way to do this would be to write a
procedural generator that would take a bag, find the bags than can
hold it, and continue onward until getting to an outermost bag. Or,
you could go the other way, and generate all possible bags held by
each bag. Or, you could do something even more fun: use graphs!
This set of produciton rules can be modeled as a graph, with x bags
contain y and z representing an edge, and the number of y and z
bags representing an edge weight. This can be done with the
NetworkX library in Python, and such a
network would look like this:
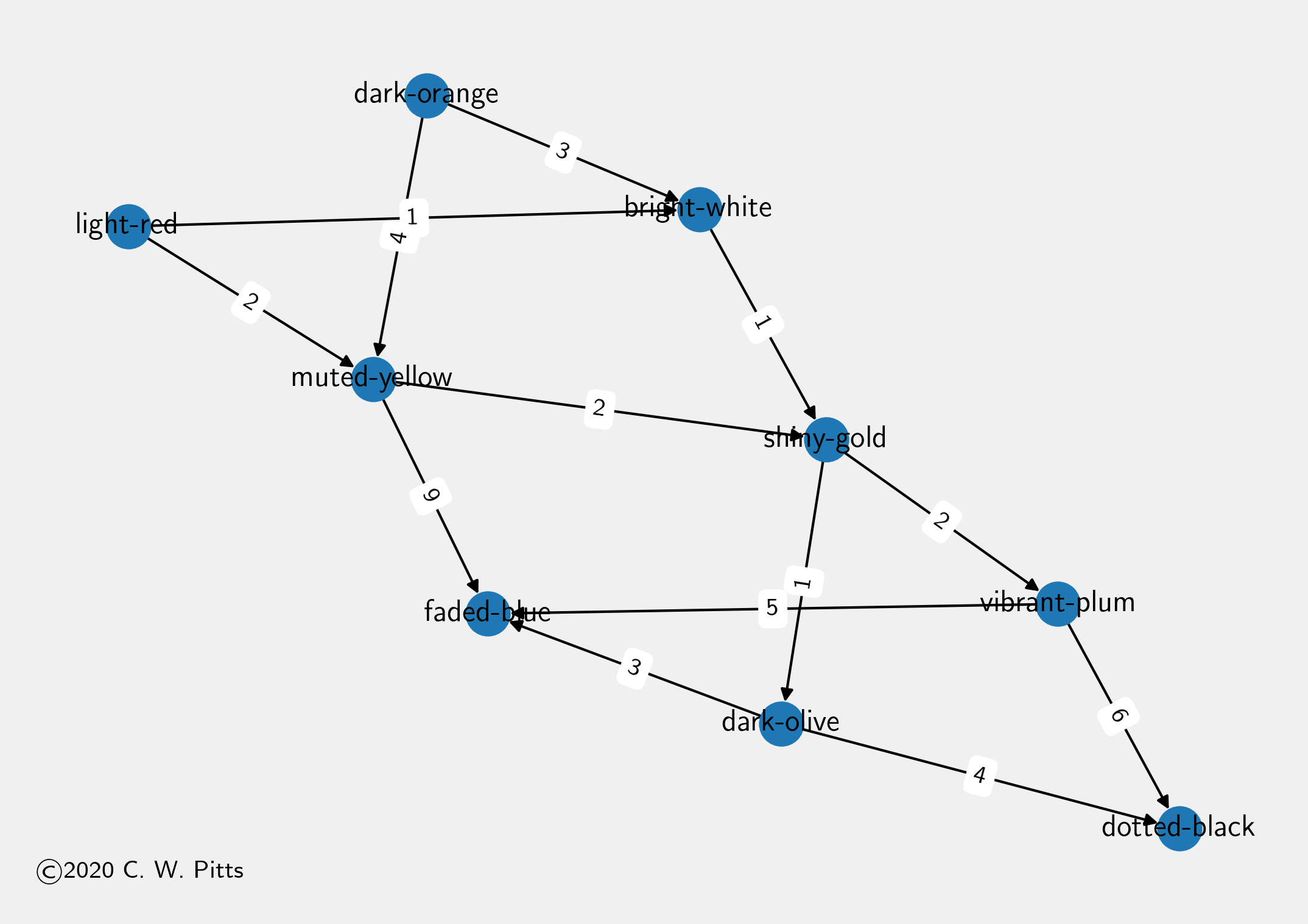
Part 1 then becomes “for how many nodes x is there a path from x to
shiny gold in the graph?” NetworkX can do this using the has_path
method, which, if you look at the
source,
uses Dijkstra’s all-pairs shortest path
algorithm.
rules = {}
with open(args.input, "r") as in_file:
# Read input
for line in in_file:
source, sinks = line.split(" contain ")
adjective, color, _ = source.split(" ")
if "no other bags" not in sinks:
produces = [part.split(" ")[:-1] for part in sinks[:-1].split(", ")]
rules[(adjective, color)] = produces
g = nx.DiGraph()
for src, dests in rules.items():
for dest in dests:
g.add_edge("-".join(src), "-".join(dest[1:]), weight=int(dest[0]))
p1 = sum(
[
nx.has_path(g, "-".join(src), "shiny-gold")
for src in rules.keys()
if src != ("shiny", "gold")
]
)
Part 2 asks for the number of bags ultimately contained in a single shiny gold bag. This is where the edge weights come into play. Each edge weight needs to be multiplied by the combined weights of each child node, and so on for the children. This can be done nicely with a recursive function:
def expand(g, node):
ret = 1
for u, v in g.edges(node):
data = g.get_edge_data(u, v)
count = data["weight"]
ret += count * expand(g, v)
return ret
This function includes the original bag, so the answer will be off by one:
p2 = expand(g, "shiny-gold") - 1