For Day 5, the puzzle consists of a series of boarding passes specify a partitioning scheme to select a seat from 128 eight-seat rows. The scheme works like this:

FBFBBFFRLR

The first 7 characters are front/back partitioning to select a row. The rest are left/right partitioning to select a seat in the row.

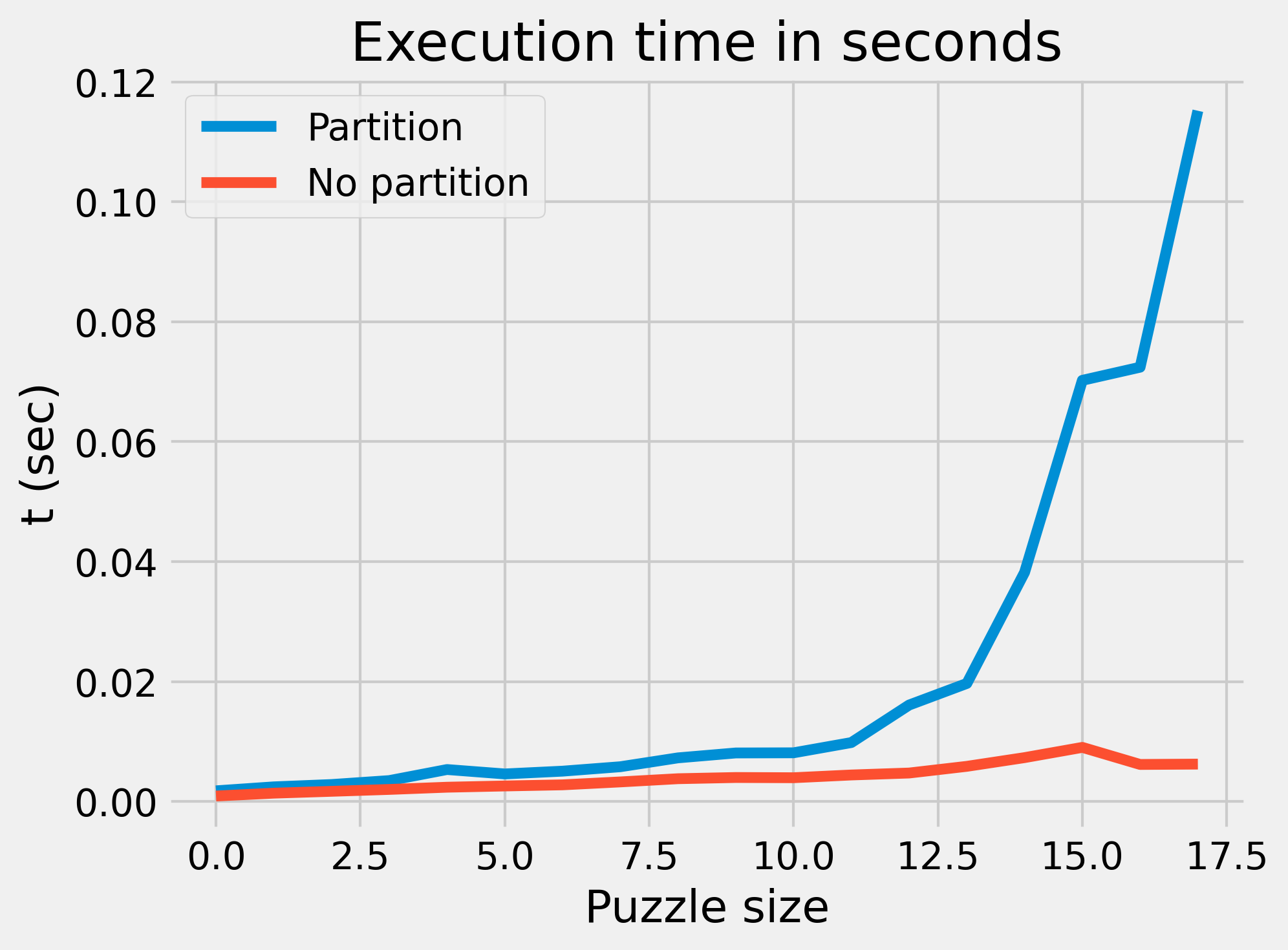
The obvious way to solve this problem is to actually use arrays, and partition them according to the instructions. Solving the puzzle this way will reveal something interesting: there is a relationship between how long the puzzle input is and how large the array is. Because the array size is set to be 128, the maximum number of one-half partitions that can be performed is $$\sqrt(128) = 7$$. Written another way, the size of the array is a power of two: $$2^{7} = 128$$. This is also true for the column array: $$2^{3} = 8$$. The array partitioning algorithm will therefore run in logarithmic time in the size of the input: $$O(\log{n})$$.

The puzzle can also be solved by keeping track of the low and high numbers at the “ends” of an imaginary array. This has the advantage of not requiring an array, but in the end the overall theoretical complexity is the same.

The runtime complexity of the two solutions, however, is rather different. Because the first solution involves directly modifying an array, it will be slower: