For Day 3 of the Advent of Code, a toboggan is sledding down a slope that extends infinitely in the horizontal place. Part 1 involves calculating the number of trees that are hit when following a slope described by $$\Delta x = 3, \Delta y = 1$$, starting from the $$(0, 0)$$ index of a grid like this (. is clear, # is a tree):

..##.......
#...#...#..
.#....#..#.
..#.#...#.#
.#...##..#.
..#.##.....
.#.#.#....#
.#........#
#.##...#...
#...##....#
.#..#...#.#

The trick for this problem is being aware of the fact that the grid extends infinitely in the horizontal plane, so the actual grid repeats after reaching the boundary of the snippet, looking more like this:

..##.........##.........##.........##....... ->
#...#...#..#...#...#..#...#...#..#...#...#.. ->
.#....#..#..#....#..#..#....#..#..#....#..#. ->
..#.#...#.#..#.#...#.#..#.#...#.#..#.#...#.# ->
.#...##..#..#...##..#..#...##..#..#...##..#. ->
..#.##.......#.##.......#.##.......#.##..... ->
.#.#.#....#.#.#.#....#.#.#.#....#.#.#.#....# ->
.#........#.#........#.#........#.#........# ->
#.##...#...#.##...#...#.##...#...#.##...#... ->
#...##....##...##....##...##....##...##....# ->
.#..#...#.#.#..#...#.#.#..#...#.#.#..#...#.# ->

One strategy for solving this is do leverage Python’s implementation of the multiplication operator for strings:

foo = "a"
print(foo * 10)
# -> aaaaaaaaaa

This can be used by calculating the needed length before reaching the bottom, and extending the string to the necessary length:

def count_trees(grid, dy, dx):
    needed_length = dx * (len(grid) // dy)
    m = math.ceil(needed_length / len(grid[0]))
    new_grid = [line * m for line in grid]

    p = [0, 0]  # y, x
    count = 0
    while p[0] < len(new_grid) - 1:
        p[0] += dy
        p[1] += dx
        if new_grid[p[0]][p[1]] == "#":
            count += 1
    return count

However, there is a more efficient solution, making use of modular arithmetic:

def better_count_trees(grid, dy, dx):
    p = [0, 0]
    count = 0
    while p[0] < len(grid) - 1:
        p[0] += dy
        p[1] += dx
        p[1] = p[1] % len(grid[0])
        if grid[p[0]][p[1]] == "#":
            count += 1

    return count

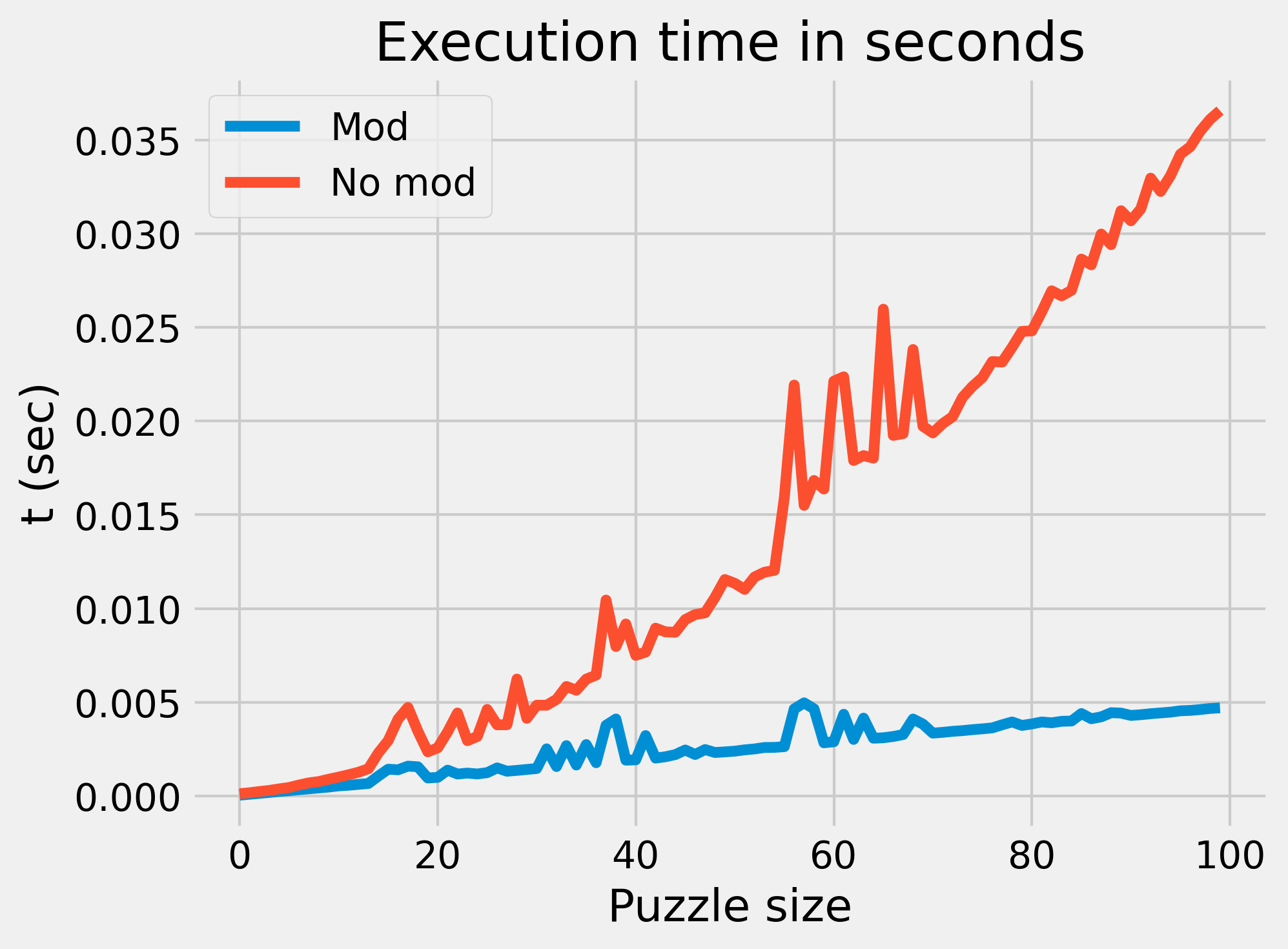
So, how much better is this faster method? I wrote a performance test that would randomly generate puzzles from depth 1 to 1000, and used the timeit module to take the average amount of time across 100 runs for each method to solve each puzzle size:

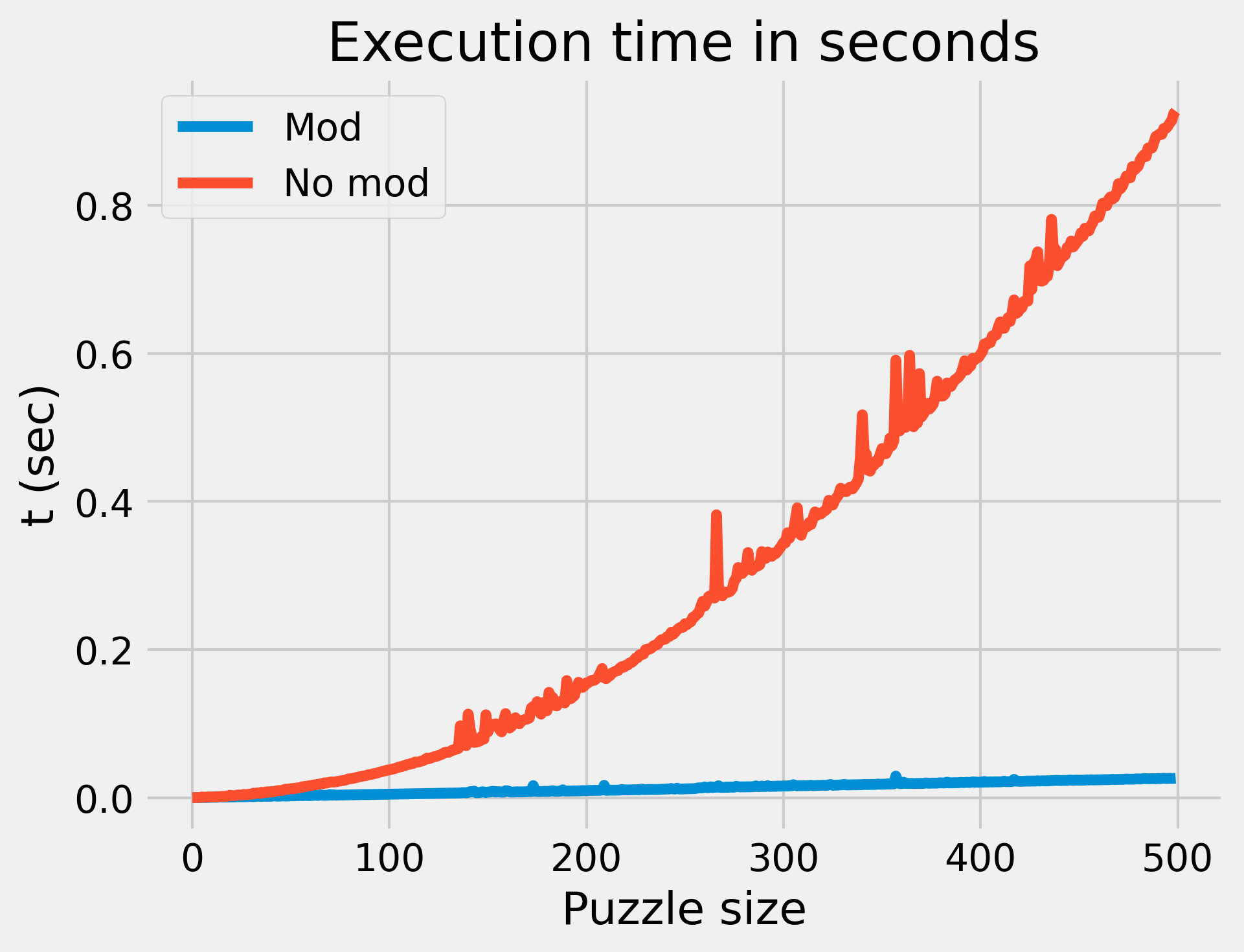
That’s a pretty stark difference. To get a better sense of the divergence, here is a set of tests that only go to 100:

The second part of the problem involves running the tree counter multiple times, for a series of $$\Delta x, \Delta y$$ slopes. This is fairly easy to do:

slopes = [(1, 1), (1, 3), (1, 5), (1, 7), (2, 1)]
hits = [
    count_trees(grid, y, x) for y, x in slopes
]
p2 = np.prod(hits)